By Ben Siraphob
During my time as a Trail of Bits associate last summer, I worked on optimizing the performance of Echidna, Trail of Bits’ open-source smart contract fuzzer, written in Haskell. Through extensive use of profilers and other tools, I was able to pinpoint and debug a massive space leak in one of Echidna’s dependencies, hevm. Now that this problem has been fixed, Echidna and hevm can both expect to use several gigabytes less memory on some test cases compared to before.
In this blog post, I’ll show how I used profiling to identify this deep performance issue in hevm and how we fixed it, improving Echidna’s performance.
Overview of Echidna
Suppose we are keeping track of a fixed supply pool. Users can transfer tokens among themselves or burn tokens as needed. A desirable property of this pool might be that supply never grows; it only stays the same or decreases as tokens are transferred or burned. How might we go about ensuring this property holds? We can try to write up some test scenarios or try to prove it by hand… or we can fuzz the code with Echidna!

How Echidna works
Echidna takes in smart contracts and assertions about their behavior that should always be true, both written in Solidity. Then, using information extracted from the contracts themselves, such as method names and constants, Echidna starts generating random transaction sequences and replaying them over the contracts. It keeps generating longer and new sequences from old ones, such as by splitting them up at random points or changing the parameters in the method calls.
How do we know that these generations of random sequences are covering enough of the code to eventually find a bug? Echidna uses coverage-guided fuzzing—that is, it keeps track of how much code is actually executed from the smart contract and prioritizes sequences that reach more code in order to create new ones. Once it finds a transaction sequence that violates our desired property, Echidna then proceeds to shrink it to try to minimize it. Echidna then dumps all the information into a file for further inspection.
Overview of profiling
The Glasgow Haskell Compiler (GHC) provides various tools and flags that programmers can use to understand performance at various levels of granularity. Here are two:
- Compiling with profiling: This modifies the compilation process to add a profiling system that adds costs to cost centers. Costs are annotations around expressions that completely measure the computational behavior of those expressions. Usually, we are interested in top-level declarations, essentially functions and values that are exported from a module.
- Collecting runtime statistics: Adding
+RTS -sto a profiled Haskell program makes it show runtime statistics. It’s more coarse than profiling, showing only aggregate statistics about the program, such as total bytes allocated in the heap or bytes copied during garbage collection. After enabling profiling, one can also use the-hToption, which breaks down the heap usage by closure type.
Both of these options can produce human- and machine-readable output for further inspection. For instance, when we compile a program with profiling, we can output JSON that can be displayed in a flamegraph viewer like speedscope. This makes it easy to browse around the data and zoom in to relevant time slices. For runtime statistics, we can use eventlog2html to visualize the heap profile.
Looking at the flamegraph below and others like it led me to conclude that at least from an initial survey, Echidna wasn’t terribly bloated in terms of its memory usage. Indeed, various changes over time have targeted performance directly. (In fact, a Trail of Bits wintern from 2022 found performance issues with its coverage, which were then fixed.) However, notice the large blue regions? That’s hevm, which Echidna uses to evaluate the candidate sequences. Given that Echidna spends the vast majority of its fuzzing time on this task, it makes sense that hevm would take up a lot of computational power. That’s when I turned my attention to looking into performance issues with hevm.

The time use of functions and call stacks in Echidna
Profilers can sometimes be misleading
Profiling is useful, and it helped me find a bug in hevm whose fix led to improved performance in Echidna (which we get to in the next section), but you should also know that it can be misleading.
For example, while profiling hevm, I noticed something unusual. Various optics-related operators (getters and setters) were dominating CPU time and allocations. How could this be? The reason was that the optics library was not properly inlining some of its operators. As a result, if you run this code with profiling enabled, you would see that the % operator takes up the vast majority of allocations and time instead of the increment function, which is actually doing the computation. This isn’t observed when running an optimized binary though, since GHC must have decided to inline the operator anyway. I wrote up this issue in detail and it helped the optics library developers close an issue that was opened last year! This little aside made me realize that I should compile programs with and without profiling enabled going forward to ensure that profiling stays faithful to real-world usage.
Finding my first huge memory leak in hevm
Consider the following program. It repeatedly hashes a number, starting with 0, and writes the hashes somewhere in memory (up to address m). It does this n times.
contract A {
mapping (uint256 => uint256) public map;
function myFunction(uint256 n, uint256 m) public {
uint256 h = 0;
for (uint i = 0; i < n; i++) {
uint256 x = h;
h = uint256(keccak256(abi.encode(h)));
map[x % m] = h;
}
}
}
What should we expect the program to do as we vary the value of n and m? If we hold m fixed and continue increasing the value of n, the memory block up to m should be completely filled. So we should expect that no more memory would be used. This is visualized below:

Holding m fixed and increasing n should eventually fill up m.
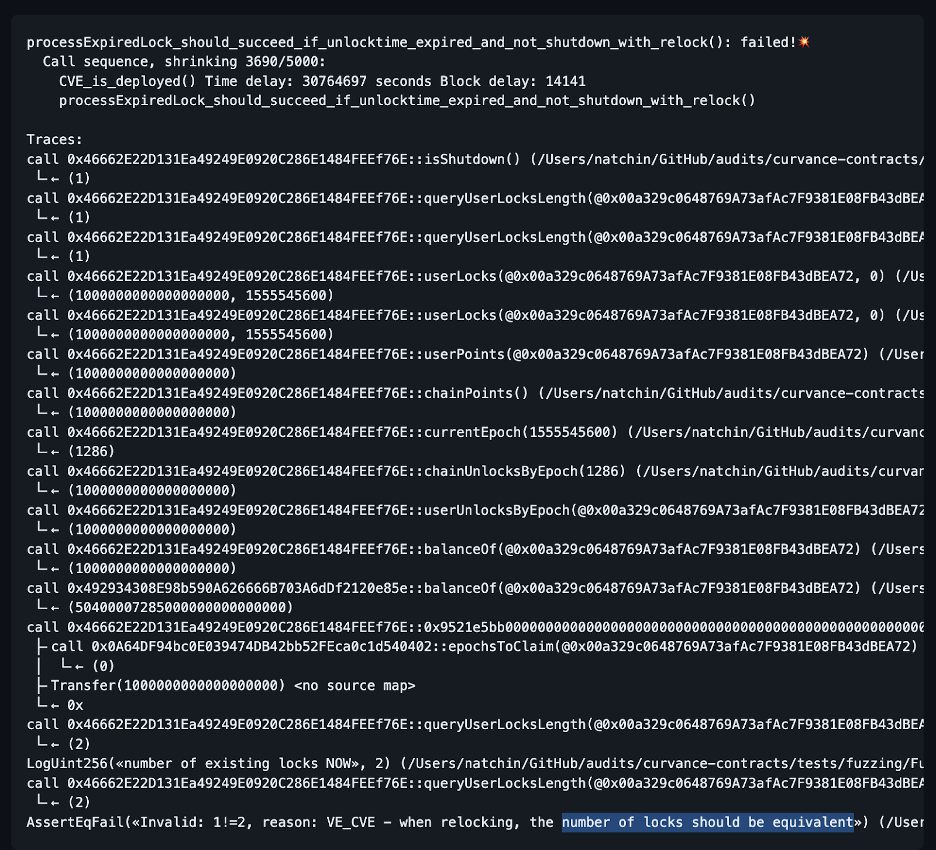
Surprisingly, this is not what I observed. The memory used by hevm went up linearly as a function of n and m. So, for some reason, hevm continued to allocate memory even though it should have been reusing it. In fact, this program used so much memory that it could use hundreds of gigabytes of RAM. I wrote up the issue here.

A graph showing allocations growing rapidly
I figured that if this memory issue affects hevm, it would surely affect Echidna as well.
Don't just measure once, measure N times!
Profiling gives you data about time and space for a single run, but that isn't enough to understand what happens as the program runs longer. For example, if you profiled Python’s insertionSort function on arrays with lengths of less than length 20, you might conclude that it's faster than quickSort when asymptotically we know that's not the case.
Similarly, I had some intuition about how "expensive" (from hevm's viewpoint) different Ethereum programs would be, but I didn’t know for sure until I measured the performance of smart contracts running on the EVM. Here's a brief overview of what smart contracts can do and how they interact with the EVM.
- The EVM consists of a stack, memory, and storage. The stack is limited to 1024 items. The memory and storage are all initialized to 0 and are indexed by an unsigned 256-bit integer.
- Memory is transient and its lifetime is limited to the scope of a transaction, whereas storage persists across transactions.
- Contracts can allocate memory in either memory or storage. While writing to storage (persistent blockchain data) is significantly more expensive gas-wise than memory (transient memory per transaction), when we're running a local node we shouldn't expect any performance differences between the two storage types.
I wrote up eight simple smart contracts that would stress these various components. The underlying commonality between all of them is that they were parameterized with a number (n) and are expected to have a linear runtime with respect to that number. Any nonlinear runtime changes would thus indicate outliers. These are the contracts and what they do:
simple_loop: Looping and adding numbersprimes: Calculation and storage of prime numbershashes: Repeated hashinghashmem: Repeated hashing and storagebalanceTransfer: Repeated transferring of 1 wei to an addressfuncCall: Repeated function callscontractCreation: Repeated contract creationscontractCreationMem: Repeated contract creations and memory
You can find their full source code in this file.
I profiled these contracts to collect information on how they perform with a wide range of n values. I increased n by powers of 2 so that the effects would be more noticeable early on. Here's what I saw:

I immediately noticed that something was definitely going on with the hashes and hashmem test cases. If the contracts’ runtimes increased linearly with increases to n, the hashes and hashmem lines wouldn't have crossed the others. How might we try to prove that? Since we know that each point should increase by roughly double (ignoring a constant term), we can simply plot the ratios of the runtimes from one point to the next and draw a line indicating what we should expect.

Bingo. hashes and hashmem were clearly off the baseline. I then directed my efforts toward profiling those specific examples and looking at any code that they depend on. After additional profiling, it seemed that repeatedly splicing and resplicing immutable bytearrays (to simulate how writes would work in a contract) caused the bytearray-related memory type to explode in size. In essence, hevm was not properly discarding the old versions of the memory.
ST to the rescue!
The fix was conceptually simple and, fortunately, had already been proposed months previously by my manager, Artur Cygan. First, we changed how hevm handles the state in EVM computations:
- type EVM a = State VM a + type EVM s a = StateT (VM s) (ST s) a
Then, we went through all the places where hevm deals with EVM memory and implemented a mutable vector that can be modified in place(!) How does this work? In Haskell, computations that manipulate a notion of state are encapsulated in a State monad, but there are no guarantees that only a single memory copy of that state will be there during program execution. Using the ST monad instead allowed us to ensure that the internal state used by the computation is inaccessible to the rest of the program. That way, hevm can get away with destructively updating the state while still treating the program as purely functional.
Here’s what the graphs look like after the PR. The slowdown in the last test case is now around 3 instead of 5.5, and in terms of actual runtime, the linearity is much more apparent. Nice!


Epilogue: Concrete or symbolic?
In the last few weeks of my associate program, I ran more detailed profilings with provenance information. Now we truly get x-ray vision into exactly where memory is being allocated in the program:

A detailed heap profile showing which data constructors use the most memory
What’s with all the Prop terms being generated? hevm has support for symbolic execution, which allows for various forms of static analysis. However, Echidna only ever uses the fully concrete execution. As a result, we never touch the constraints that hevm is generating. This is left for future work, which will hopefully lead to a solution in which hevm can support a more optimized concrete-only mode without compromising on its symbolic aspects.
Final thoughts
In a software project like Echidna, whose effectiveness is proportional to how quickly it can perform its fuzzing, we’re always looking for ways to make it faster without making the code needlessly complex. Doing performance engineering in a setting like Haskell reveals some interesting problems and definitely requires one to be ready to drop down and reason about the behavior of the compilation process and language semantics. It is an art as old as computer science itself.
We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%.
— Donald Knuth